CRÉATIVITÉ ENFANTINE ET MATHÉMATIQUES

CRÉATIVITÉ ENFANTINE ET MATHÉMATIQUES

La créativité intervient à différents niveaux dans l’enseignement des mathématiques. L’incitation à la créativité constitue un maillon important de la méthode de recherche sur les processus d’abstraction de concepts mathématiques; on s’aperçoit, d’autre part, que la créativité intervient dans le processus d’abstraction lui-même. Enfin, l’analyse des créations des enfants constitue un excellent moyen de contrôle des acquisitions.

On constate que la mathématique constitue un domaine tout à fait particulier où peut s’exercer la créativité.

Recherche sur l’enseignement des mathématiques et créativité

Le vaste mouvement de réforme de l’enseignement des mathématiques a été l’occasion de recherches sur la façon dont de jeunes enfants abordent, abstraient des concepts mathématiques; on a voulu, en particulier, mettre au clair des progressions et des méthodes qui suivent au mieux les activités mentales spontanées de l’enfant et les utilisent. Pour pouvoir poursuivre de telles recherches, il faut évidemment que l’adulte expérimentateur influence l’enfant le moins possible par des suggestions quant aux façons de faire, sinon on observerait l’aptitude de l’enfant à se conformer à un mode de pensée adulte et l’adéquation ou l’inadéquation de la construction qu’échafaude l’adulte pour faire acquérir une notion donnée. Une bonne méthode consiste donc à soumettre aux enfants des problèmes ouverts qui doivent susciter leur recherche, leur activité intellectuelle, puis à observer, étudier, analyser les productions orales et écrites des enfants.

Les recherches qui ont été effectuées avec ce type de méthode ont mis en évidence que la quasi-totalité des enfants éprouve un grand goût pour la recherche, aime inventer. Cette constatation a été faite avec des enfants issus de régions et de milieux culturels variés.

On constate très souvent que les méthodes utilisées par les enfants pour venir à bout d’une situation donnée diffèrent notablement des prévisions établies par les adultes en fonction du bagage de concepts considérés comme acquis par des enfants. Cela s’explique par le fait que l’équipement mental de l’enfant est constitué à la fois d’un bagage de concepts et d’un bagage de savoir-faire, savoir-utiliser. Or, si le bagage de concepts peut être à peu près correctement établi, le bagage de savoir-faire est beaucoup plus difficile à mettre au clair. Une recherche fondée sur la créativité de l’enfant peut permettre à l’éducateur de ne pas faire d’erreur grossière quant à la progression à travers les notions. Il se peut qu’elle fournisse un mode d’approche tout aussi mathématique que le mode d’approche envisagé par l’adulte, mais plus en accord avec le mode de pensée de l’enfant.

Nous prendrons pour exemple la résolution d’équations . On avait constaté une très grande difficulté chez beaucoup d’enfants de première année du cours moyen à admettre l’équivalence des deux propositions suivantes:

L’expérimentateur justifiait l’équivalence par des exemples relevant de la proposition: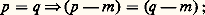

cela était finalement admis par les enfants, puis utilisé comme une règle.

Or, un jour, l’un d’entre eux proposa de «transformer en machine» ce qu’il écrivit pour l’équation proposée x + 8 = 17:

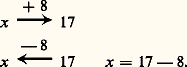La méthode fut immédiatement adoptée par tous les enfants; l’expression «transformer en machine», que n’aurait certainement utilisée spontanément aucun adulte, fut comprise et adoptée par tous. Cette méthode fut ensuite proposée par l’expérimentateur avec succès à une autre classe, mais on constata qu’aucun enfant ne passa directement de la proposition x + a = b à la proposition x = b 漣 a . Tous avaient besoin, comme phase intermédiaire, de «transformer en machine». On passa ensuite sans difficulté à la résolution d’équations telles que:

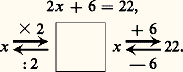On peut ensuite résoudre des systèmes d’équations linéaires à deux inconnues, alors qu’un essai avec proposition, par l’expérimentateur, de la «méthode de substitution» s’était soldé par un échec total dans trois classes.

La figure 1 présente des propositions de résolution du système:

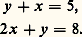La notion d’intersection va fournir un second exemple. Dès le cours préparatoire, on donne aux enfants de petits problèmes consistant à poser «à la place convenable» des objets sur un diagramme tels que le suivant:

On s’aperçoit que, si tous les enfants savent rapidement réussir cet exercice, peu sont capables de faire spontanément un diagramme représentant une intersection. Il y a ensuite apprentissage; presque tous les enfants réussissent. Mais on constate l’année suivante qu’il y a aussi apprentissage puis oubli. Cela s’explique à partir de l’analyse de productions d’enfants de deuxième année du cours moyen qui met en évidence que, dans le mode de pensée de l’enfant, l’algèbre des propositions est un préalable à l’algèbre des ensembles: on aura donc intérêt à présenter comme moyen d’expression des tables de vérité plutôt que des diagrammes de Venn. Dans l’exercice de la figure 2, on demandait à des enfants de deuxième année du cours élémentaire de faire un schéma (dans l’esprit de l’expérimentateur un diagramme de Venn) où l’on verrait chacun à une place convenable: les nombres plus grands que 3 et plus petits que 23, les multiples de 2, les multiples de 10.

Dans ces deux cas, la recherche fondée sur l’analyse des productions des enfants permet donc de substituer à la stratégie prévue initialement par l’adulte une stratégie plus conforme au mode spontané de fonctionnement de l’esprit de l’enfant; cette nouvelle stratégie satisfait d’ailleurs tout autant l’adulte que la première qui était envisagée. Elle peut être employée par les maîtres, sans effort d’adaptation.

Il n’en est pas toujours ainsi. Les processus utilisés par les enfants sont souvent plus compliqués que ceux qu’auraient proposés les adultes. En effet, il apparaît qu’un progrès consiste fréquemment en une simplification des savoir-faire, un savoir-faire abandonné étant éliminé, comme oublié, au bénéfice d’un autre savoir-faire plus performant, plus automatisable. Or l’expérience montre qu’il est peu efficace et souvent nuisible de court-circuiter la phase où l’on utilise des moyens d’action «compliqués»; le passage à un moyen simple doit être fait par l’intéressé lui-même si l’on veut que ce moyen soit réellement intégré, donc utilisable (cf. la résolution d’équations présentée dans le premier exemple). Or, l’oubli du savoir-faire primitif met l’adulte en difficulté pour communiquer avec l’enfant. En effet, même si, par son observation, il a élaboré un mode d’approche en accord avec les structures mentales de l’enfant, il ne peut en parler, le dire que comme quelque chose d’étranger à sa propre façon de penser. La communication, au contraire, se fait très bien entre enfants: le langage-mots, organisation de la phrase exprimant directement la pensée actuelle de celui qui a trouvé une solution, est compris de celui qui n’a pas trouvé cette solution. Celui qui communique donne le fruit de son expérience personnelle. Il ne joue pas un rôle.

La mise en état de créativité, qui apparaît nécessaire dans le cadre de la recherche, s’avère donc également nécessaire comme moyen pédagogique dès que l’on ne se contente pas de l’apprentissage de règles, c’est-à-dire quand on considère que l’enseignement des mathématiques n’a pas uniquement pour but de munir les élèves d’outils utiles mais aussi de les aider à se constituer un équipement mental efficace.

L’utilisation de la créativité comme moyen pédagogique

Nécessité d’une pédagogie active

Nous venons de voir que, dans certains cas, pour qu’une découverte se fasse, il est nécessaire que l’enfant passe par certains processus étrangers au mode de pensée de l’adulte. La meilleure façon de procéder est, alors, de laisser chercher les enfants et de les faire échanger entre eux pour se communiquer des manières de faire qui leur sont propres, et cela dans leur langage, même si ce langage n’est pas celui qu’utiliserait le mathématicien. Il y a davantage. Lorsqu’une recherche est achevée, une certaine progression est établie et l’on pourrait penser que, puisque cette progression est conforme à l’évolution de la pensée de l’enfant, quelle que soit la pédagogie choisie, les notions proposées devraient être normalement intégrées. En effet, une méthode suscitant la créativité de l’enfant pourrait être perçue comme ne s’imposant que dans la perspective de l’observation de la pensée spontanée de l’enfant. Une fois la phase de recherche terminée, certains maîtres reprennent des méthodes traditionnelles pour l’enseignement dans leur propre classe et ne font guère appel à l’activité personnelle des enfants, à leur initiative, aux nécessaires tâtonnements, aux erreurs mêmes, ce qui est inhérent à toute recherche: cette dernière manière de faire apparaît comme trop coûteuse en temps. Or, on a constaté un niveau d’intégration beaucoup plus faible dans de telles classes que dans les autres classes parallèles de la même école où les maîtres pratiquent une pédagogie active.

Nous en prendrons un exemple au niveau de la deuxième année du cours élémentaire. Après expérimentation, il était apparu que la meilleure façon d’introduire des expressions de la forme «a 憐 b » et «a : b » était d’utiliser des «machines à multiplier» et des «machines à diviser». Le dispositif de base comporte une entrée, une machine, une sortie et il est schématisé comme suit:

La «machine à multiplier par n » est celle qui, pour tout objet de l’entrée, produit n objets à la sortie.

La «machine à diviser par n » est présentée comme «défaisant le travail de la machine à multiplier par n », c’est-à-dire que, pour tout paquet de n objets à l’entrée, la machine restitue un objet à la sortie.

Après des manipulations, on représente les situations par des schémas tels que les suivants:

Les machines peuvent être mises en chaîne:

On va, à partir de cela, découvrir après bien des essais les règles de composition de telles machines, les règles d’«alimentation» des chaînes comportant des machines à diviser. Si on laisse ces découvertes à l’initiative des enfants, cela demande beaucoup de temps, si bien que des maîtres pensent qu’il est plus rentable de mécaniser les règles, ce qui leur donne l’occasion de faire faire aux enfants beaucoup de calcul mental et donne des résultats immédiats spectaculaires. Mais on constate l’année suivante qu’il y a eu oubli des règles: la chaîne 憐 3憐 2est souvent considérée comme équivalente à 憐 5 轢. La récupération est difficile, car il faut revenir au point de départ (ce qui, psychologiquement, est toujours pénible à accepter), revenir aux manipulations et aux schémas qui apparaissent aux enfants comme une régression.

Utiliser ou construire l’outil mathématique

De nombreuses situations expérimentales ont permis de mettre en évidence le fait que savoir se servir d’un outil mathématique ne signifie pas que l’on a intégré ni même perçu cet outil.

Nous en prendrons un exemple au niveau du cours élémentaire, première année. On avait fourni aux enfants un arbre permettant de colorier les cartes d’un jeu. Chaque carte représente un oiseau pour lequel l’arbre indique la coloration de la tête, de la queue, du corps. Alors que tous les enfants avaient été capables d’utiliser l’arbre sans aucune explication, un seulement sur vingt-sept a su reconstituer l’arbre pour expliquer à un camarade absent comment avait été colorié le jeu de cartes: de l’arbre, il n’avaient retenu, comme sur la figure 3, que les cheminements effectués pour colorier chaque carte. Un enfant ayant suggéré plus tard de «faire un vrai arbre pour faire monter les petits oiseaux», l’expérimentateur suggéra de faire un arbre tel qu’au bout de chaque branche il y ait un nid et dans chaque nid uniquement des oiseaux de même couleur. Les enfants cherchèrent donc comment fabriquer un tel arbre; l’un eut l’idée de «mettre des panneaux de signalisation aux embranchements» pour indiquer «par quelle branche chaque oiseau devait monter». L’arbre fut fabriqué correctement et l’on constata par la suite que des schémas en arbre furent utilisés spontanément dans des situations très diverses, tel l’arbre de la figure 4 réalisé par une petite fille du cours élémentaire, première année, voulant expliquer les activités faites pendant deux semaines à partir de l’étude du hérisson.

Créativité et liberté d’expression

Pour permettre la créativité, il est nécessaire de fournir aux enfants une grande variété de moyens d’expression (des schémas divers): ne pas affecter systématiquement tel type de schéma à tel type de situation, car la perception des situations n’est pas la même pour tous; ne pas juger de la «valeur» de tel ou tel schéma par rapport à d’autres présentés par d’autres enfants; ne pas être trop exigeant, dans un premier temps, quant à la correction de l’écriture, l’obsession de la correction bloquant souvent de bonnes initiatives.

On s’aperçoit qu’une expression – une représentation – qui nous apparaît pauvre est souvent confrontée avec d’autres représentations; cette confrontation est source de découvertes que des représentations jugées plus riches n’auraient sans doute pas permis de faire.

Nous en prendrons un exemple au niveau de la deuxième année du cours moyen.

La situation proposée était la suivante: des boules rouges et bleues étaient dans un sac; on tirait ces boules une à une; la question posée était: «Représenter par un schéma ce que l’on constate.» Treize types de schémas furent fournis par les vingt-huit enfants d’une classe. La figure 5 en donne trois exemples.

Le niveau des représentations exprimées sur la figure 5 est très différent, et l’adulte donne évidemment une préférence très nette pour la représentation 5 b. Or un enfant qui avait fait un schéma du type 5 c, voyant le tableau fait par son camarade 5 b, eut l’idée suivante: «Si je sais ce que j’ai dans un sac au départ, je peux chercher toutes les façons possibles de sortir les pions: il suffit qu’à chaque fois je fasse un trait de chaque couleur»; c’est donc en fait l’idée de sa représentation très primitive, associée à celle de son camarade de représenter le contenu du sac par un couple, qui lui a donné l’idée de se poser un nouveau problème et la possibilité de le résoudre (fig. 6).

On voit dans cet exemple l’intérêt de la liberté d’expression et de l’absence de jugement sur la valeur du mode d’expression. Un éloge trop grand du schéma 5 b au détriment de 5 a ou 5 c eût bloqué la faculté d’invention de l’auteur du schéma considéré comme peu intéressant.

La créativité comme moyen de contrôle

Il est souvent très difficile pour le maître de savoir ce qui est passé d’une notion qu’il a cherché à faire acquérir par ses élèves. En effet, les exercices de contrôle d’acquisition sont souvent très trompeurs. Un enfant qui a compris la notion peut donner un pourcentage élevé de réponses fausses pour des raisons diverses; un enfant qui n’a pas compris la notion peut donner un pourcentage élevé de réponses justes parce qu’il se sera fabriqué une heuristique qui ne fait pas appel à l’intégralité de la notion et qui statistiquement donne de bons résultats: lorsque l’on passera à une nouvelle notion faisant référence à la notion précédente, il y aura alors souvent échec inexpliqué. Une bonne façon de voir ce qui a été acquis d’une notion est de demander aux enfants d’inventer des exercices sur cette notion, les mécompréhensions apparaissent alors très clairement (fig. 2 et 3). Le critère qu’une notion est acquise est la possibilité d’une utilisation spontanée (fig. 4 et 6).

La mathématique comme domaine de créativité

On sait que la possibilité de créer est indispensable à la formation de la personnalité. De nombreuses activités peuvent fournir l’occasion de créer – tout ce qui relève de l’art en particulier: dans une pédagogie de l’initiative, les activités artistiques tiennent une place importante. On signalera aussi toutes les activités de type artisanal qui font intervenir des techniques dans lesquelles il est possible d’innover, qui obligent à inventer des dispositifs nouveaux. La mathématique offre, elle aussi, un champ pour la créativité. En mathématique, créer présente cette particularité que le créateur peut être juge objectif de sa création, ce qui n’est pas le cas dans le domaine de l’art.

La possibilité de créer en mathématique exige d’avoir de l’imagination, de l’intuition; cela suppose que l’on est capable de se poser des problèmes (fig. 6) et de les résoudre en utilisant des outils que l’on n’avait, jusque-là, jamais utilisés ensemble. La création en mathématique fait évidemment appel à des processus différents de ceux de la création artistique; en particulier, elle exige l’enchaînement logique, et il est intéressant de remarquer que, si le choix des règles de jeu posées au départ (les axiomes) est totalement libre, une fois ces règles posées, leur auteur doit s’y tenir et ne peut plus en changer en cours de route. Il est évident qu’un enfant respectera d’autant mieux les règles que c’est lui-même, ou son groupe de travail, qui les aura posées. Donner aux enfants la possibilité de créer en mathématique va donc leur permettre non seulement d’abstraire des concepts mathématiques, mais de développer leurs aptitudes à imagination et à intuition – qu’ils possèdent presque tous – et de s’initier à la rigueur, ce qu’ils n’ont l’occasion de faire dans la vie non scolaire que lorsqu’ils jouent à des jeux à règles que peu d’entre eux pratiquent à l’école actuelle: dames, cartes, échecs, go, etc.

Encyclopédie Universelle. 2012.